07- Splines and Generalized Addive Models Code Demo

R implementation

birthrates <- read.csv("../data/birthrates.csv")

Polynomial regression

lmfit3 <- lm(Birthrate ~ poly(Year-mean(Year), degree = 3), data = birthrates)
plot(birthrates, pch = 19, col = 4, main = "degree = 3")
lines(birthrates$Year, lmfit3$fitted.values, lty = 1, col = 2, lwd = 2)

Cubic Splines

library(splines)

For linear splines, change degree = 3 to degree = 1.

cub_sp <- lm(Birthrate ~ splines::bs(Year, degree = 3, knots = c(1936, 1960, 1978)), 
             data = birthrates)
plot(birthrates, pch = 19, col = 4, main = "Cubic spline (k = 3) with 3 knots")
lines(birthrates$Year, cub_sp$fitted.values, lty = 1, col = 2, lwd = 3)

Smoothing Splines

fit <- smooth.spline(birthrates$Year, birthrates$Birthrate, df = 15)
plot(birthrates$Year, birthrates$Birthrate, pch = 19, 
     xlab = "Year", ylab = "BirthRates", col = 4)
lines(seq(1917, 2003), predict(fit, seq(1917, 2003))$y, col = 2, lty = 1, lwd = 3)

GAM

library(gam)

Loading required package: foreach

Loaded gam 1.22-4

Wage <- read.csv("../data/Wage.csv")
Wage$education <- as.factor(Wage$education)
gam.m3 <- gam(wage ~ s(year, df = 4) + s(age , df = 5) + education, data = Wage)
par(mfrow = c(1, 3), mar = c(4, 4, 2, 0))
plot.Gam(gam.m3, se = TRUE, col = 4, lwd = 2, las = 1)

Python implementation

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt

birthrates = pd.read_csv("../data/birthrates.csv")

Polynomial regression

from sklearn.linear_model import LinearRegression
from sklearn.preprocessing import PolynomialFeatures

birthrates['Year_centered'] = birthrates['Year'] - birthrates['Year'].mean()

# Polynomial regression with degree = 3
poly = PolynomialFeatures(degree=3, include_bias=False)
X_poly = poly.fit_transform(birthrates[['Year_centered']])

polyfit3 = LinearRegression().fit(X_poly, birthrates['Birthrate'])

plt.scatter(birthrates['Year'], birthrates['Birthrate'], color='blue')
plt.plot(birthrates['Year'], polyfit3.predict(X_poly), color='red',
         linewidth=2)
plt.title("Cubic Polynomial Regression (Degree = 3)")
plt.xlabel("Year")
plt.ylabel("Birthrate")
plt.show()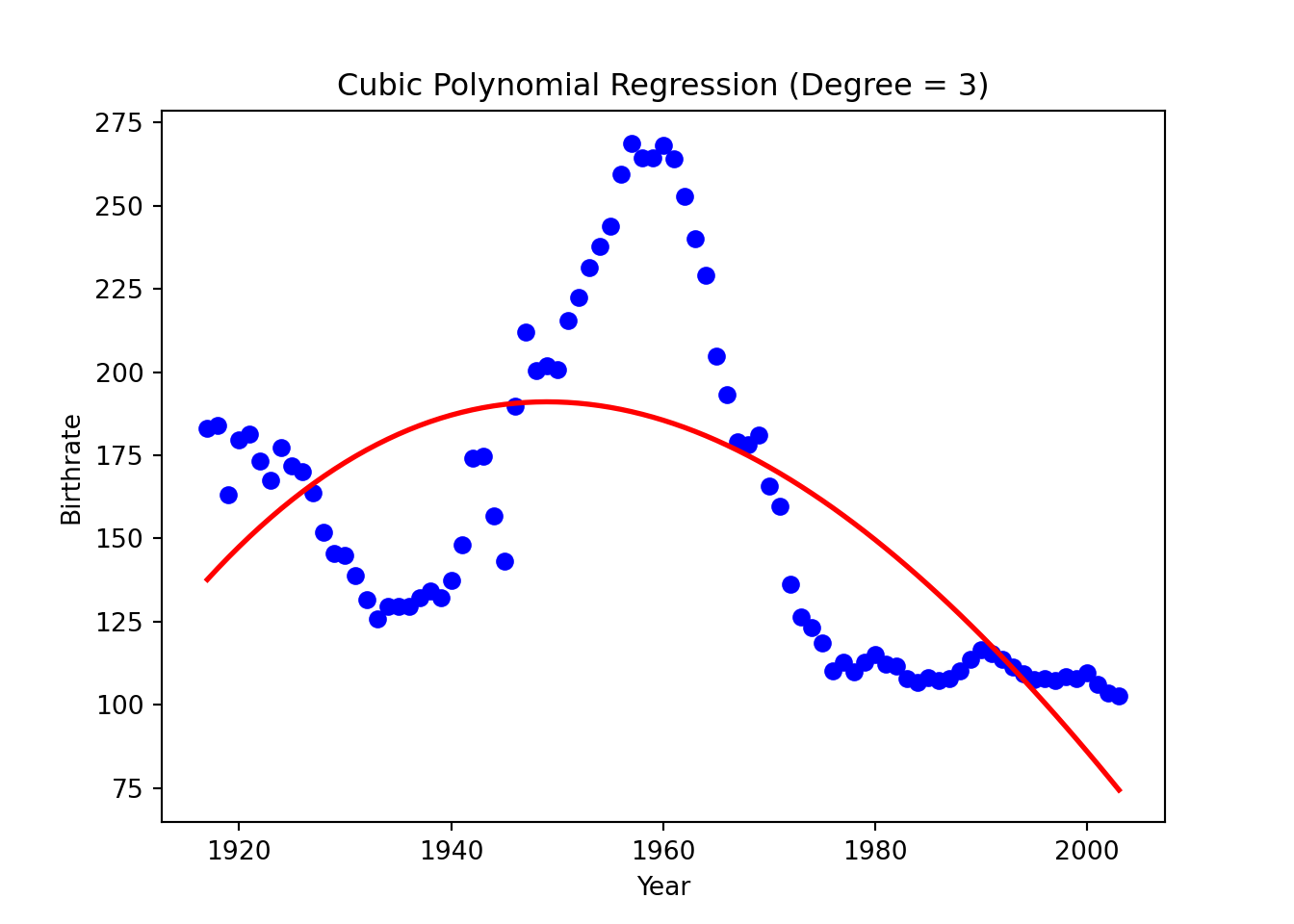

Cubic Splines

from patsy import dmatrix
from sklearn.linear_model import LinearRegression

For linear splines, change degree=3 to degree=1.

NOTE:

• Can’t find prediction or extrapolation for cubic splines.

• Use patsy.cr() to fit natural cubic splines.

knots = [1936, 1960, 1978]
# https://patsy.readthedocs.io/en/latest/API-reference.html
# Generate cubic spline basis functions with specified knots
spline_basis = dmatrix(
    "bs(Year, degree=3, knots=knots, include_intercept=True)", 
    {"Year": birthrates["Year"]}, 
    return_type="dataframe"
)
# Fit the cubic spline model
# import statsmodels.api as sm
# model = sm.OLS(birthrates["Birthrate"], spline_basis).fit()
# birthrates["Fitted"] = model.fittedvalues
cub_sp = LinearRegression().fit(spline_basis, birthrates["Birthrate"])

# Plot the data and the fitted spline
plt.scatter(birthrates["Year"], birthrates["Birthrate"], color="blue")
plt.plot(birthrates["Year"], cub_sp.predict(spline_basis), color="red",
         linewidth=2)
plt.title("Cubic Spline (d=3) with 3 Knots")
plt.xlabel("Year")
plt.ylabel("Birthrate")
plt.show()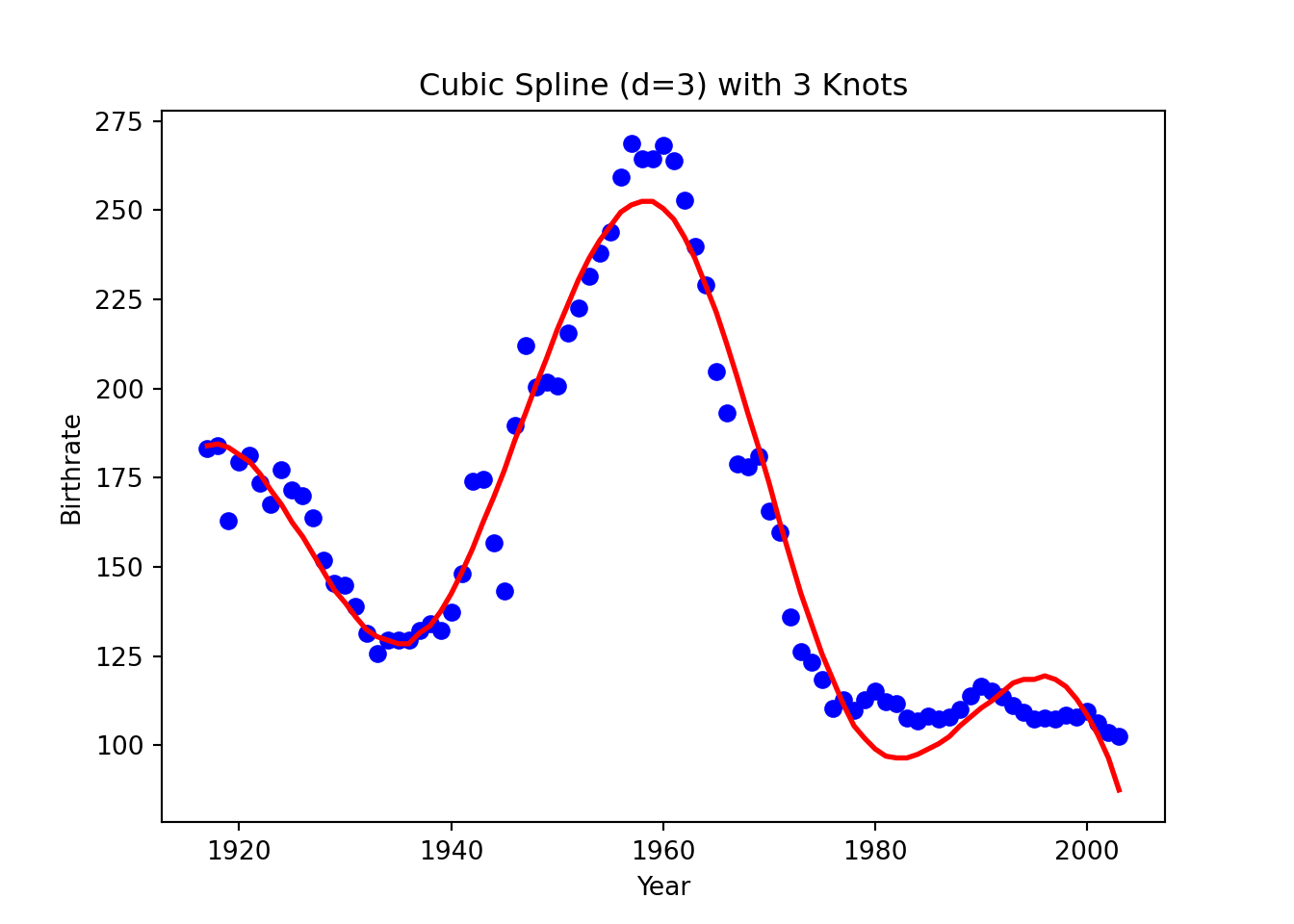

# https://patsy.readthedocs.io/en/latest/API-reference.html
# Generate cubic spline basis functions with specified knots
spline_basis = dmatrix(
    "bs(Year, degree=3, df=7, include_intercept=True)", 
    {"Year": birthrates["Year"]}, 
    return_type="dataframe"
)
# Fit the cubic spline model
# import statsmodels.api as sm
# model = sm.OLS(birthrates["Birthrate"], spline_basis).fit()
# birthrates["Fitted"] = model.fittedvalues
cub_sp = LinearRegression().fit(spline_basis, birthrates["Birthrate"])

# Plot the data and the fitted spline
plt.scatter(birthrates["Year"], birthrates["Birthrate"], color="blue")
plt.plot(birthrates["Year"], cub_sp.predict(spline_basis), color="red",
         linewidth=2)
plt.title("Cubic Spline (df=6)")
plt.xlabel("Year")
plt.ylabel("Birthrate")
plt.show()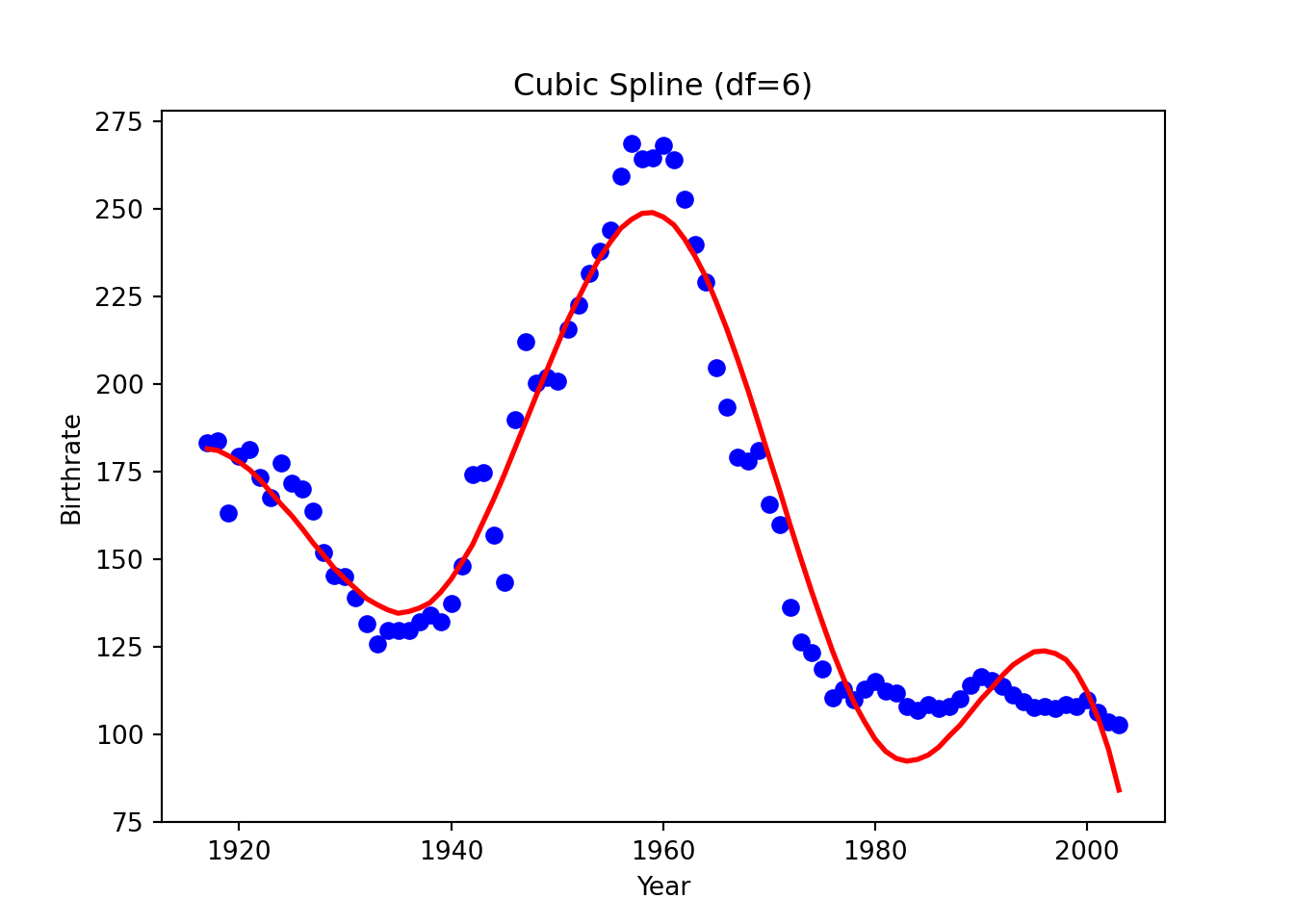

Smoothing Splines

We use scipy.interpolate.make_smoothing_spline.

• Python has no functions for smoothing splines that can directly specify the degrees of freedom. Please let me know if you find one.

• To have similar smoothing results, R and Python would use quite a different size of penalty term \(\lambda\), as well as the degrees of freedom and smoothing factor.

from scipy.interpolate import make_smoothing_spline

x = birthrates["Year"].values
y = birthrates["Birthrate"].values
spline = make_smoothing_spline(x, y, lam=20)
# Predict for the range of years
x_pred = np.linspace(1917, 2003, 500)
y_pred = spline(x_pred)
# Plot the original data
plt.figure(figsize=(10, 6))
plt.scatter(x, y, color='blue', label='Data', s=50)
plt.plot(x_pred, y_pred, color='red', linewidth=3, label='Smoothing Spline')
plt.title("Smoothing Spline")
plt.xlabel("Year")
plt.ylabel("Birthrate")
plt.show()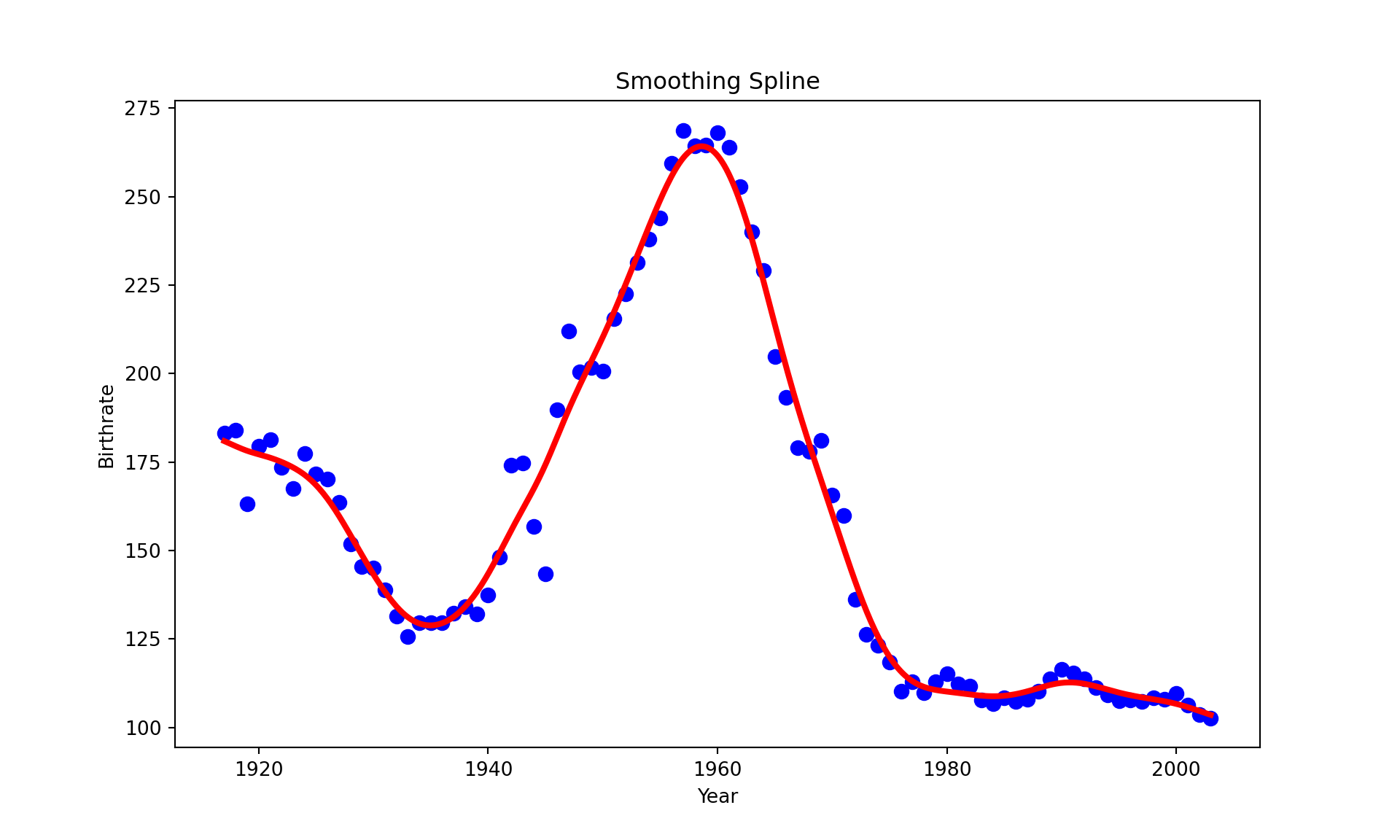

To use a smoothing factor, use splrep (make_splrep) and BSpline

The smoothing factor is set unresonably high to 4500. Please let me know if you figure out why.

from scipy.interpolate import splrep, BSpline

x = birthrates["Year"].values
y = birthrates["Birthrate"].values

# Fit the smoothing spline with a smoothing factor
smoothing_factor = 4500 # Adjust this for the desired smoothness
tck = splrep(x, y, s=smoothing_factor)

# Predict for a range of years
x_pred = np.linspace(1917, 2003, 500)
y_pred = BSpline(*tck)(x_pred)

# Plot the original data
plt.figure(figsize=(10, 6))
plt.scatter(x, y, color='blue', label='Data', s=50)

# Plot the fitted smoothing spline
plt.plot(x_pred, y_pred, color='red', linewidth=3, label='Smoothing Spline')

# Add labels and title
plt.title("Smoothing Spline with splrep")
plt.xlabel("Year")
plt.ylabel("Birthrate")
plt.show()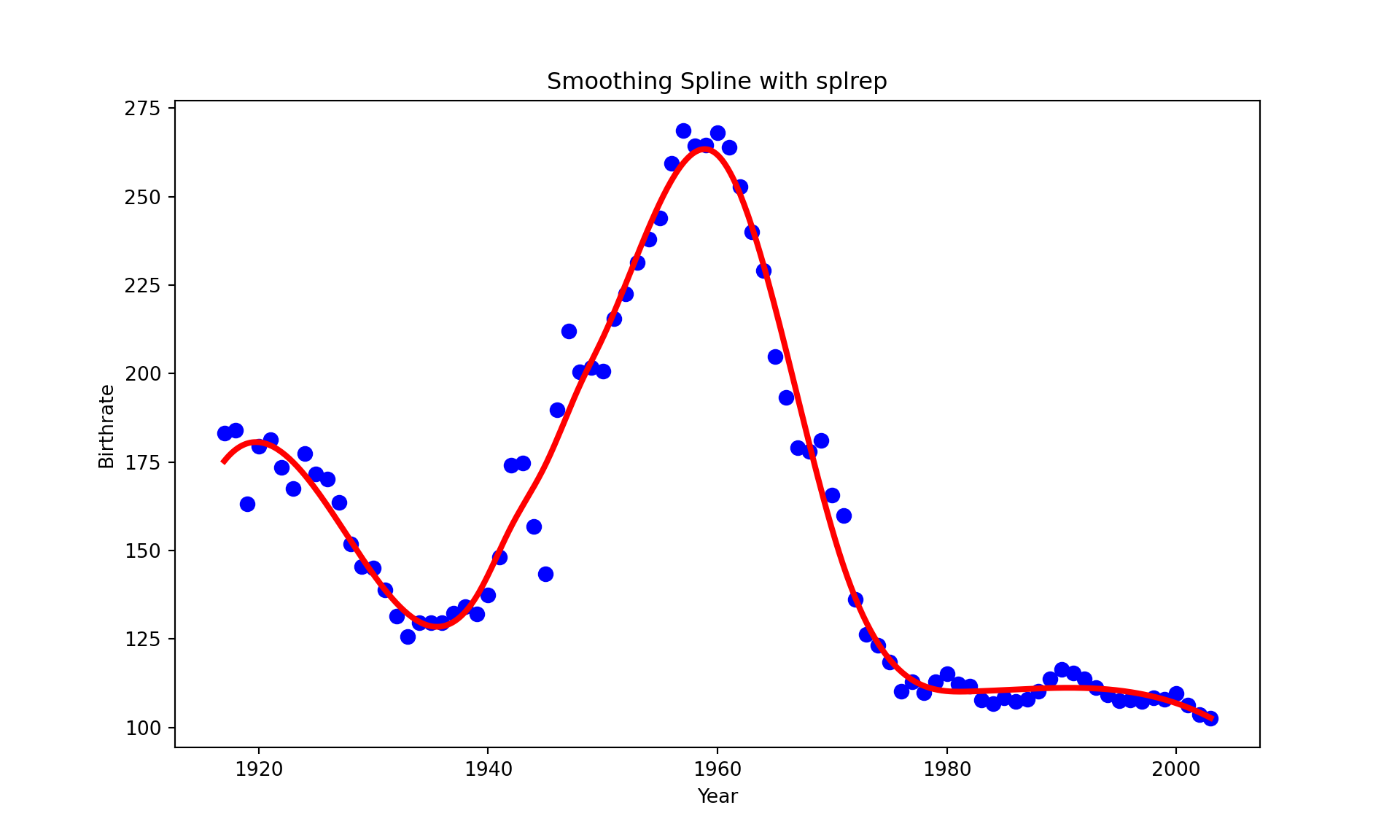

GAM

https://kirenz.github.io/regression/docs/gam.html

https://gist.github.com/josef-pkt/453de603b019143e831fbdd4dfb6aa30

from statsmodels.gam.api import BSplines
from statsmodels.gam.api import GLMGam
from statsmodels.tools.eval_measures import mse, rmse
import statsmodels.api as sm
import patsy

Wage = pd.read_csv("../data/Wage.csv")
Wage['education'] = pd.Categorical(Wage['education'], categories=['1. < HS Grad', '2. HS Grad', '3. Some College', '4. College Grad', '5. Advanced Degree'], ordered=True)

# penalization weights are taken from mgcv to match up its results
# sp = np.array([0.830689464223685, 425.361212061649])
# s_scale = np.array([2.443955e-06, 0.007945455])
x_spline = Wage[['year', 'age']].values
exog = patsy.dmatrix('education', data=Wage)

# TODO: set `include_intercept=True` automatically if constraints='center'
bs = BSplines(x_spline, df=[4, 5], degree=[3, 3], variable_names=['year', 'age'], 
              constraints='center', include_intercept=True)
# alpha = 1 / s_scale * sp / 2
gam_bs = GLMGam(Wage['wage'], exog=exog, smoother=bs)
res = gam_bs.fit()

fig, axes = plt.subplots(1, 2, figsize=(12, 6))
res.plot_partial(0, cpr=False, include_constant=False, ax=axes[0])
axes[0].set_title("Year")
res.plot_partial(1, cpr=False, include_constant=False, ax=axes[1])
axes[1].set_title("Age")
plt.tight_layout()
plt.show()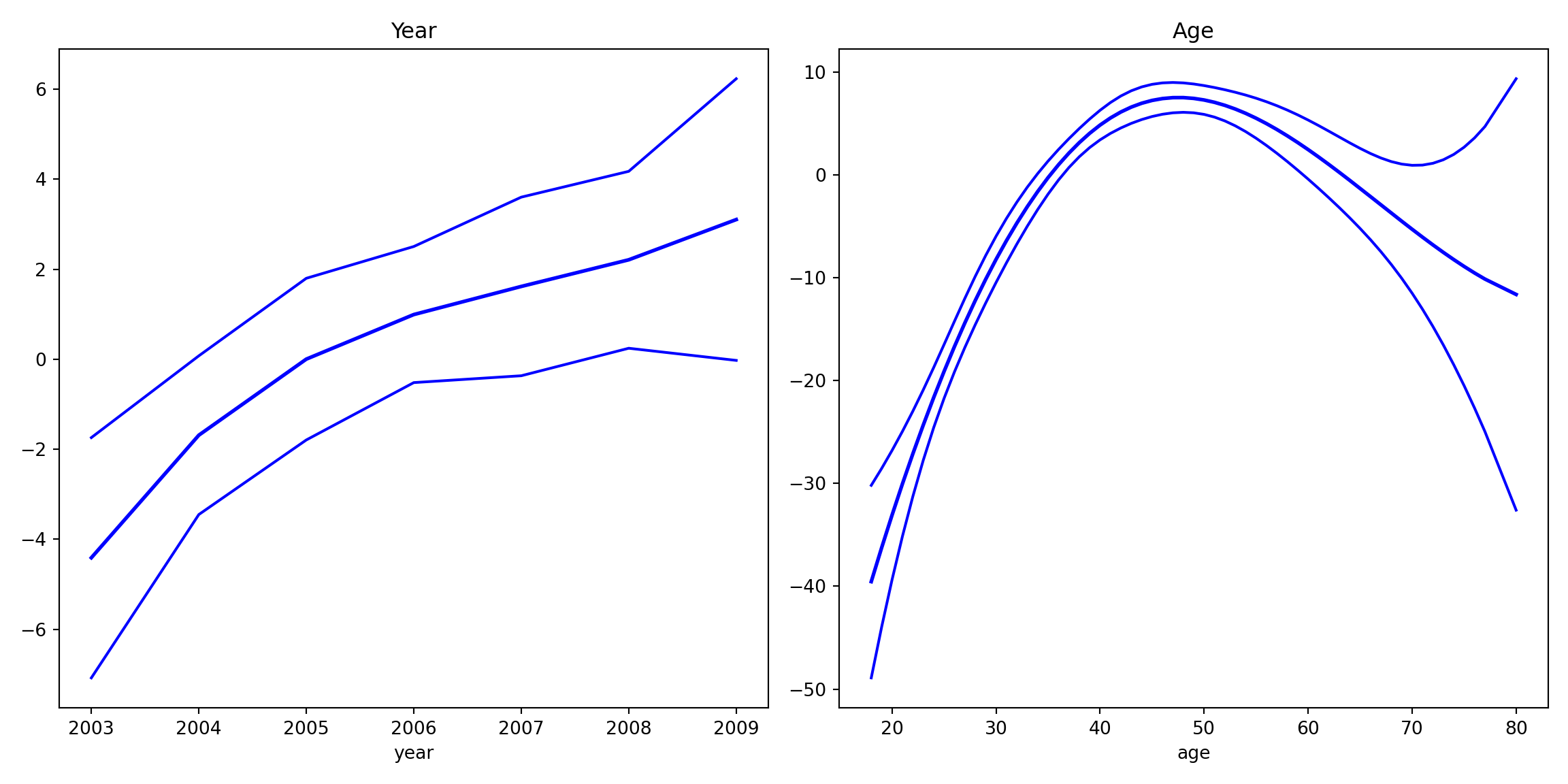

print(res.summary())

                 Generalized Linear Model Regression Results                  
==============================================================================
Dep. Variable:                   wage   No. Observations:                 3000
Model:                         GLMGam   Df Residuals:                     2988
Model Family:                Gaussian   Df Model:                        11.00
Link Function:               Identity   Scale:                          1238.8
Method:                         PIRLS   Log-Likelihood:                -14934.
Date:                Mon, 10 Feb 2025   Deviance:                   3.7014e+06
Time:                        21:43:15   Pearson chi2:                 3.70e+06
No. Iterations:                     3   Pseudo R-squ. (CS):             0.3358
Covariance Type:            nonrobust                                         
===================================================================================================
                                      coef    std err          z      P>|z|      [0.025      0.975]
---------------------------------------------------------------------------------------------------
Intercept                          85.6860      2.156     39.745      0.000      81.461      89.911
education[T.2. HS Grad]            10.7413      2.431      4.418      0.000       5.977      15.506
education[T.3. Some College]       23.2067      2.563      9.056      0.000      18.184      28.229
education[T.4. College Grad]       37.8704      2.547     14.871      0.000      32.879      42.862
education[T.5. Advanced Degree]    62.4355      2.764     22.591      0.000      57.019      67.852
year_s0                             3.3874      4.257      0.796      0.426      -4.957      11.732
year_s1                             1.8170      4.220      0.431      0.667      -6.454      10.088
year_s2                             4.4943      1.754      2.563      0.010       1.057       7.931
age_s0                             10.1360      5.932      1.709      0.087      -1.490      21.762
age_s1                             47.6380      5.326      8.945      0.000      37.200      58.076
age_s2                              6.7739      7.296      0.928      0.353      -7.526      21.074
age_s3                            -10.0472     10.672     -0.941      0.346     -30.963      10.869
===================================================================================================

One option is to use pygam package.

from pygam import LinearGAM, s, f
from pygam.datasets import wage

X, y = wage(return_X_y=True)

## model
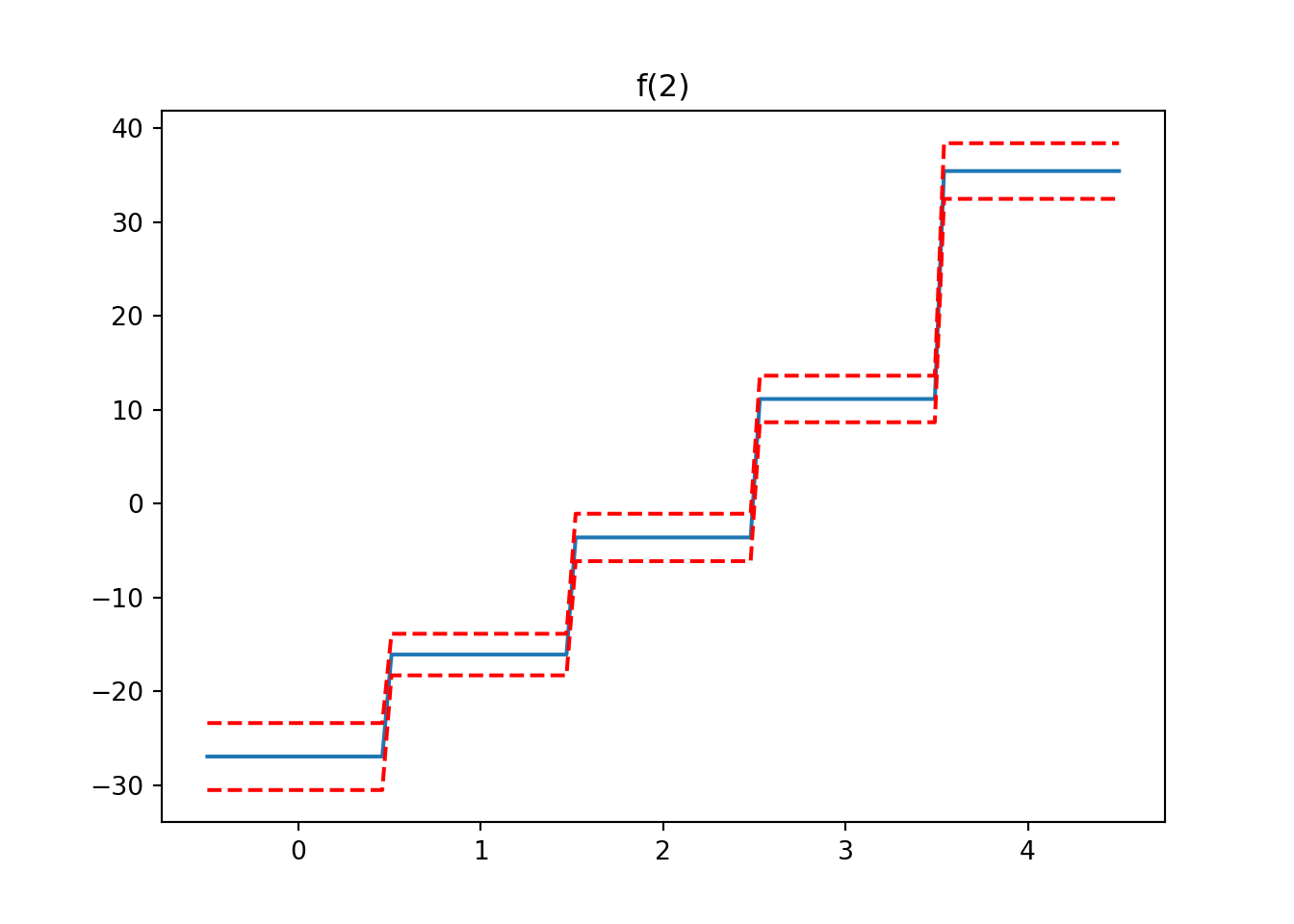
gam = LinearGAM(s(0) + s(1) + f(2)).fit(X, y)

for i, term in enumerate(gam.terms):
    if term.isintercept:
        continue

    XX = gam.generate_X_grid(term=i)
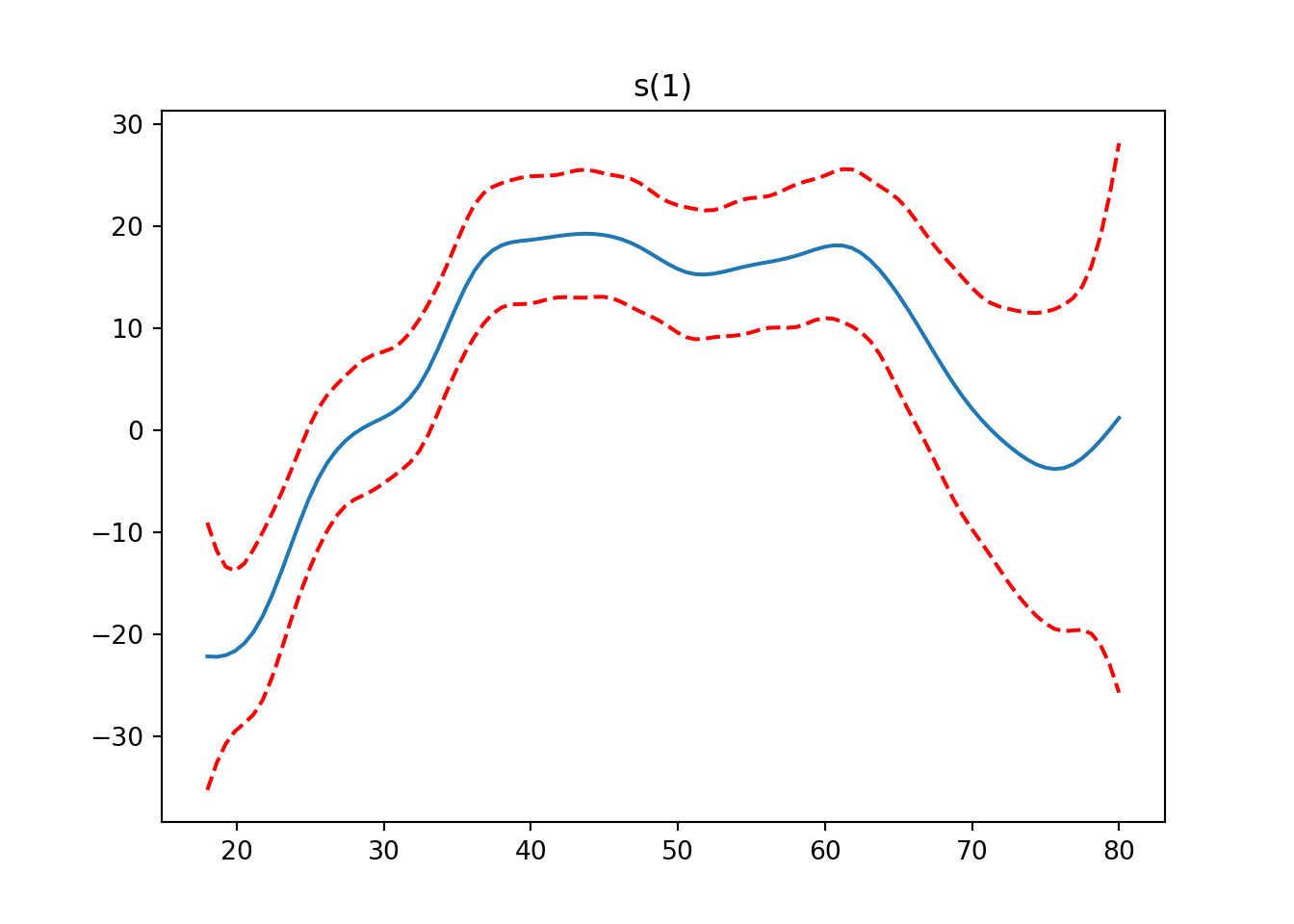
    pdep, confi = gam.partial_dependence(term=i, X=XX, width=0.95)

    plt.figure()
    plt.plot(XX[:, term.feature], pdep)
    plt.plot(XX[:, term.feature], confi, c='r', ls='--')
    plt.title(repr(term))
    plt.show()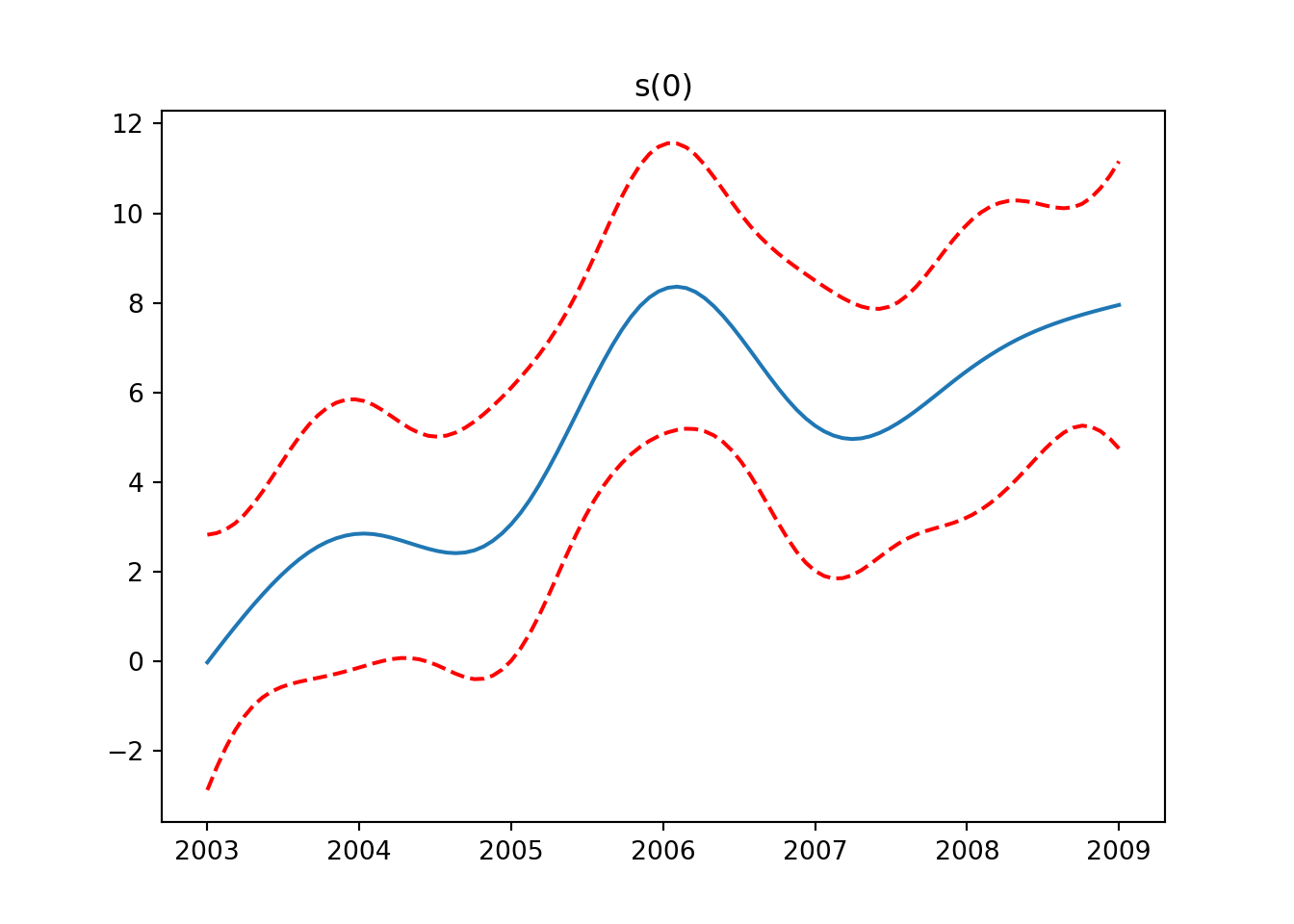

gam.summary()

LinearGAM                                                                                                 
=============================================== ==========================================================
Distribution:                        NormalDist Effective DoF:                                     25.1911
Link Function:                     IdentityLink Log Likelihood:                                -24118.6847
Number of Samples:                         3000 AIC:                                            48289.7516
                                                AICc:                                           48290.2307
                                                GCV:                                             1255.6902
                                                Scale:                                           1236.7251
                                                Pseudo R-Squared:                                   0.2955
==========================================================================================================
Feature Function                  Lambda               Rank         EDoF         P > x        Sig. Code   
================================= ==================== ============ ============ ============ ============
s(0)                              [0.6]                20           7.1          5.95e-03     **          
s(1)                              [0.6]                20           14.1         1.11e-16     ***         
f(2)                              [0.6]                5            4.0          1.11e-16     ***         
intercept                                              1            0.0          1.11e-16     ***         
==========================================================================================================
Significance codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

WARNING: Fitting splines and a linear function to a feature introduces a model identifiability problem
         which can cause p-values to appear significant when they are not.

WARNING: p-values calculated in this manner behave correctly for un-penalized models or models with
         known smoothing parameters, but when smoothing parameters have been estimated, the p-values
         are typically lower than they should be, meaning that the tests reject the null too readily.
<string>:3: UserWarning: KNOWN BUG: p-values computed in this summary are likely much smaller than they should be. 
 
Please do not make inferences based on these values! 

Collaborate on a solution, and stay up to date at: 
github.com/dswah/pyGAM/issues/163