16 - Clustering Code Demo

Author

Dr. Cheng-Han Yu

1 R implementation

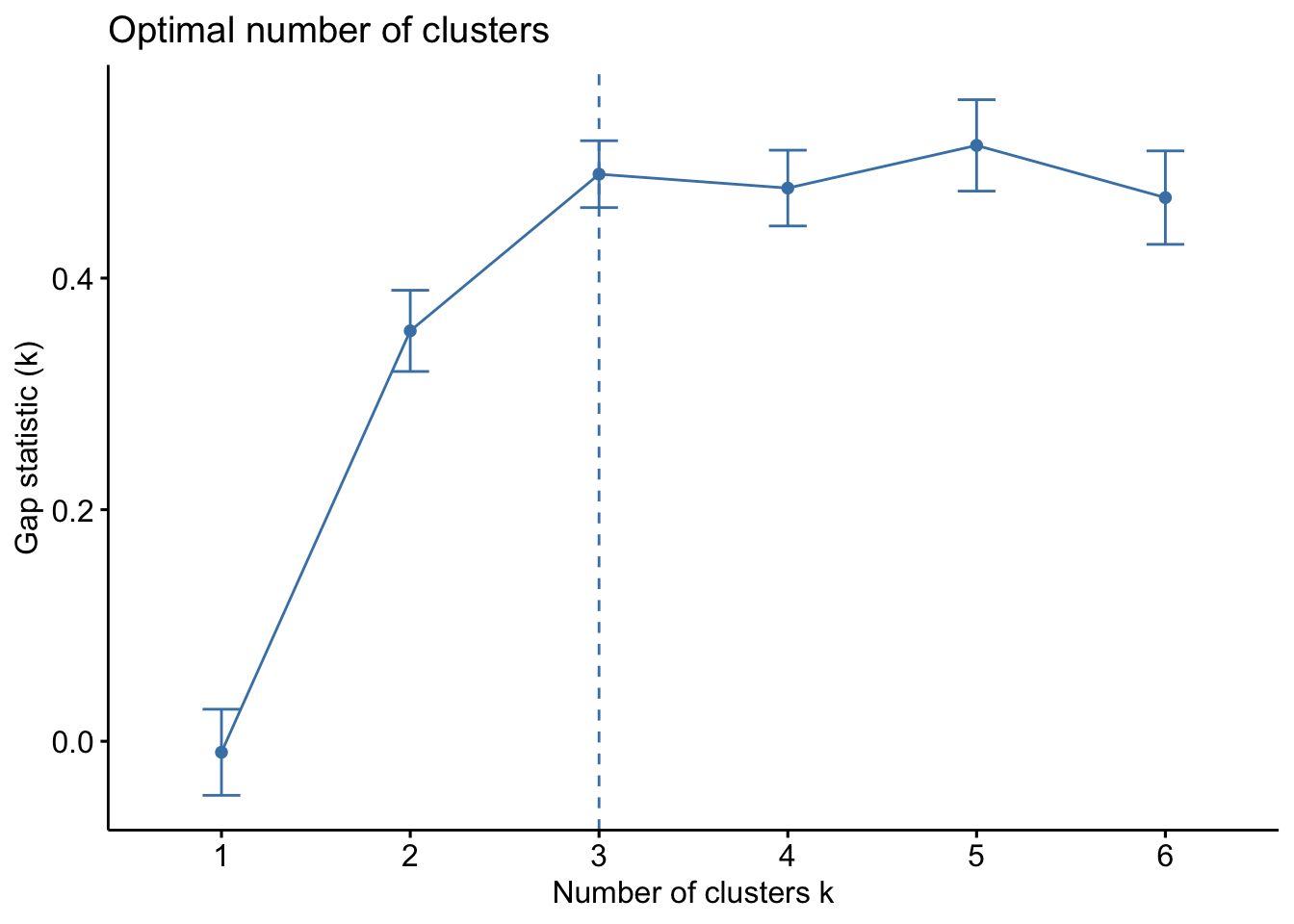
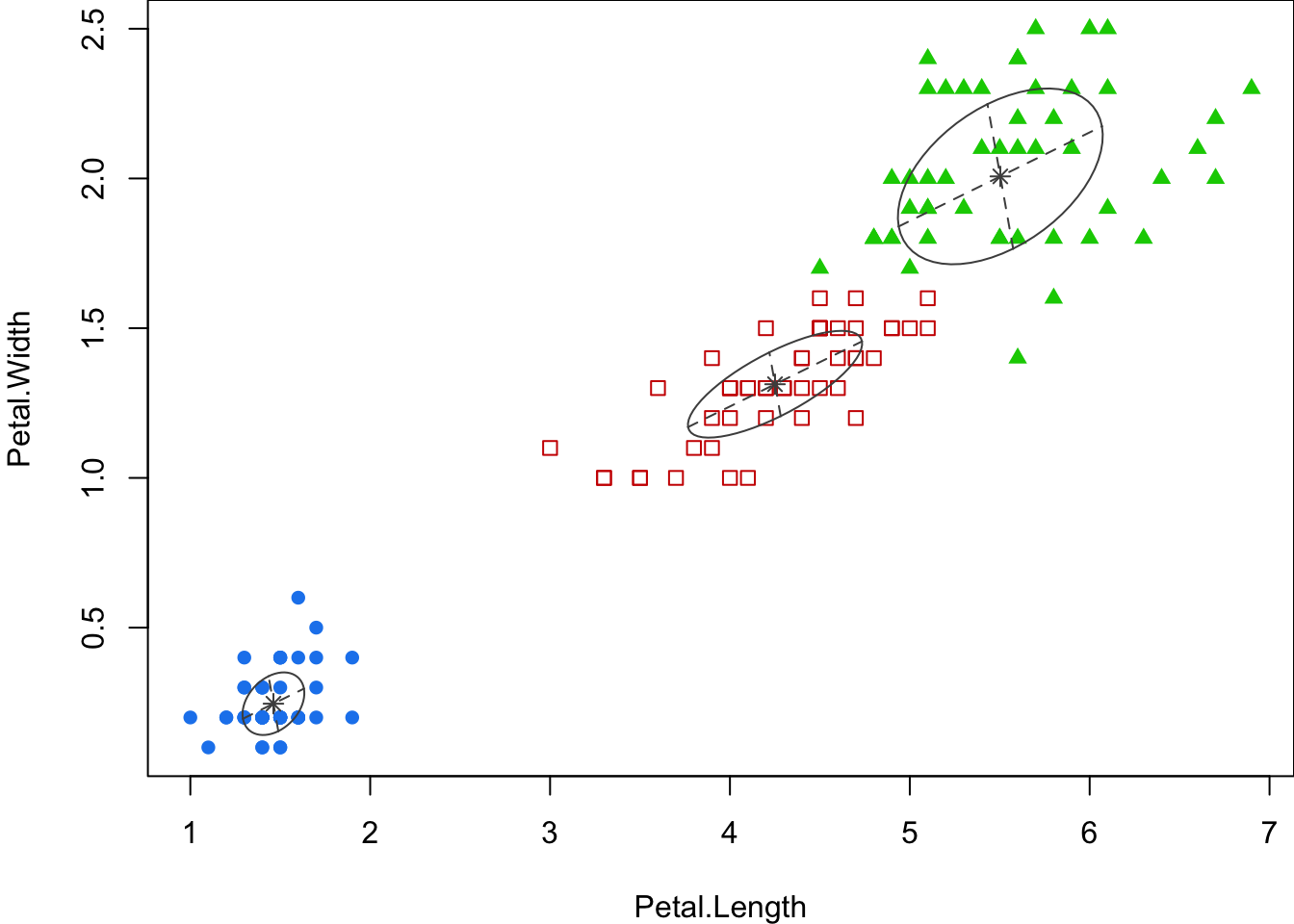
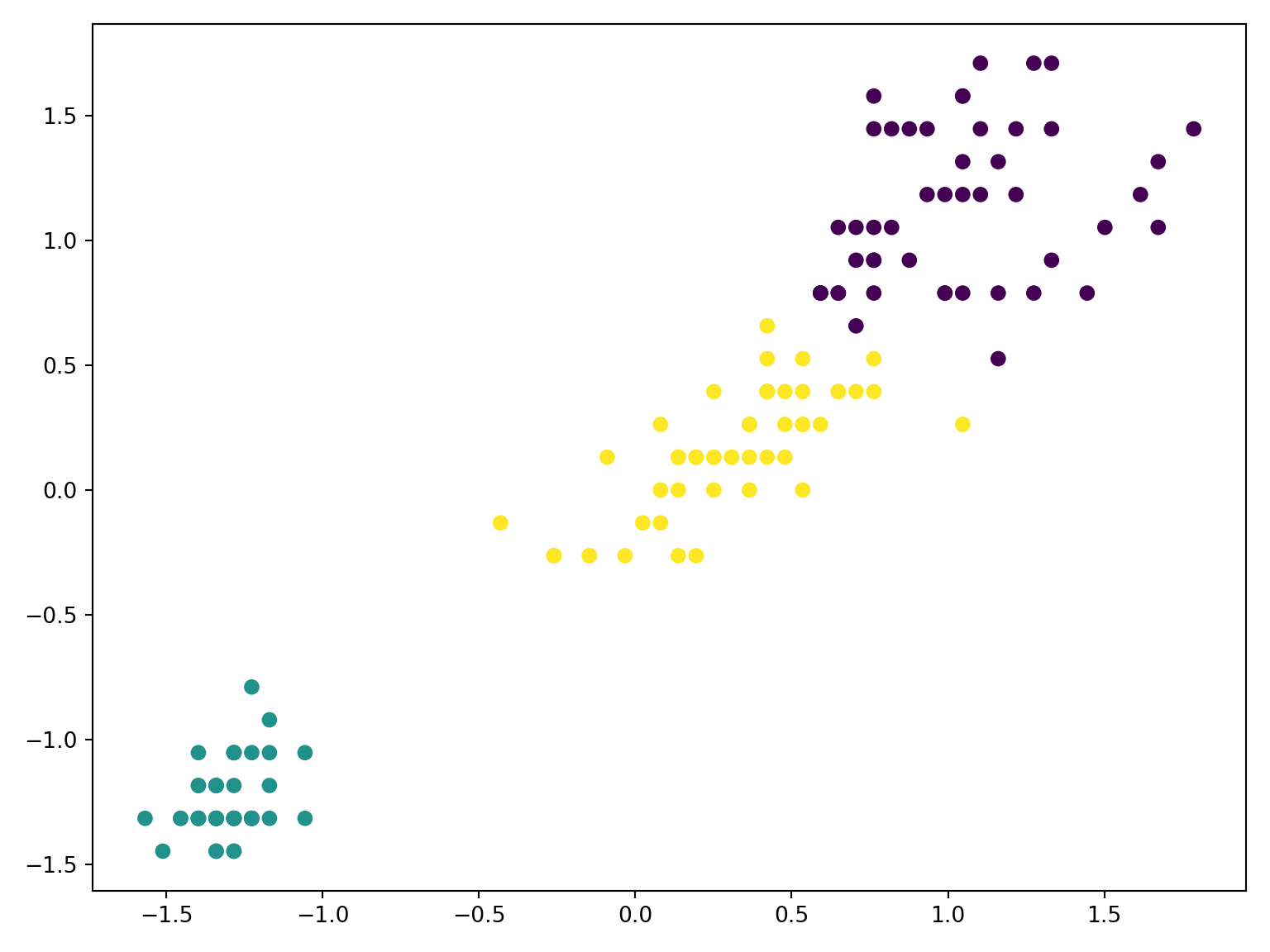
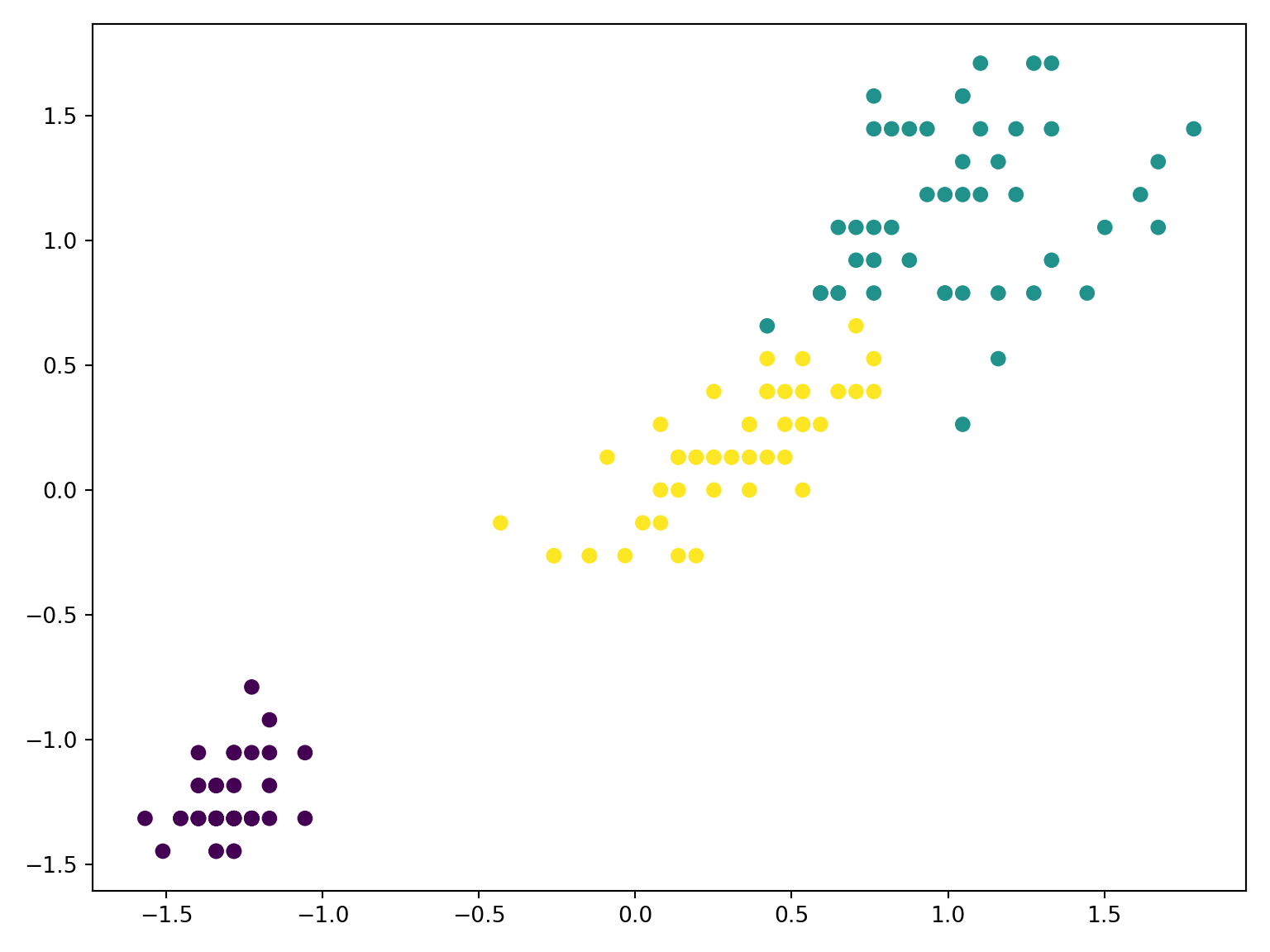
Code

head(iris, 10)

   Sepal.Length Sepal.Width Petal.Length Petal.Width Species
1           5.1         3.5          1.4         0.2  setosa
2           4.9         3.0          1.4         0.2  setosa
3           4.7         3.2          1.3         0.2  setosa
4           4.6         3.1          1.5         0.2  setosa
5           5.0         3.6          1.4         0.2  setosa
6           5.4         3.9          1.7         0.4  setosa
7           4.6         3.4          1.4         0.3  setosa
8           5.0         3.4          1.5         0.2  setosa
9           4.4         2.9          1.4         0.2  setosa
10          4.9         3.1          1.5         0.1  setosa

1.1 K-Means

Code

df_clust <- iris[, 3:4]
(iris_kmean <- kmeans(df_clust, centers = 3, nstart = 20))

K-means clustering with 3 clusters of sizes 50, 48, 52

Cluster means:
  Petal.Length Petal.Width
1     1.462000    0.246000
2     5.595833    2.037500
3     4.269231    1.342308

Clustering vector:
  [1] 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
 [38] 1 1 1 1 1 1 1 1 1 1 1 1 1 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3
 [75] 3 3 3 2 3 3 3 3 3 2 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 2 2 2 2 2 2 3 2 2 2 2
[112] 2 2 2 2 2 2 2 2 3 2 2 2 2 2 2 3 2 2 2 2 2 2 2 2 2 2 2 3 2 2 2 2 2 2 2 2 2
[149] 2 2

Within cluster sum of squares by cluster:
[1]  2.02200 16.29167 13.05769
 (between_SS / total_SS =  94.3 %)

Available components:

[1] "cluster"      "centers"      "totss"        "withinss"     "tot.withinss"
[6] "betweenss"    "size"         "iter"         "ifault"

Code

library(factoextra)

Loading required package: ggplot2

Welcome! Want to learn more? See two factoextra-related books at https://goo.gl/ve3WBa

Code

fviz_cluster(object = iris_kmean, data = df_clust, label = NA)

Code

## wss =  total within sum of squares
fviz_nbclust(x = df_clust, FUNcluster = kmeans, method = "wss",  k.max = 6)

Code

fviz_nbclust(x = df_clust, FUNcluster = kmeans, method = "silhouette",  k.max = 6)

Code

fviz_nbclust(df_clust, kmeans, method = "gap_stat",  k.max = 6)

1.2 Gaussian-Mixture-Model (GMM) based Clustering

Code

library(mclust)

Package 'mclust' version 6.1.1
Type 'citation("mclust")' for citing this R package in publications.

Code

gmm_clus <- Mclust(df_clust)
par(mar = c(4, 4, 0, 0))
plot(gmm_clus, what = "classification")

2 Python implementation

2.1 K-Means

Code

import numpy as np
import pandas as pd
from sklearn.cluster import KMeans
from sklearn.preprocessing import StandardScaler

Code

from sklearn.datasets import load_iris
iris = load_iris(as_frame=True)

Code

scaler = StandardScaler()
X = scaler.fit_transform(iris.data.iloc[:, [2, 3]])

Code

kmeans = KMeans(n_clusters=3,  n_init=10).fit(X)
kmeans.labels_[0:10]

array([1, 1, 1, 1, 1, 1, 1, 1, 1, 1], dtype=int32)

Code

kmeans.cluster_centers_

array([[ 1.02799959,  1.12797813],
       [-1.30498732, -1.25489349],
       [ 0.3058728 ,  0.16541778]])

Code

# y_pred = KMeans(n_clusters=3,  n_init=10).fit_predict(X)
import matplotlib.pyplot as plt
plt.figure(figsize=(8, 6))
plt.scatter(X[:, 0], X[:, 1], c=kmeans.labels_)
plt.tight_layout()

2.2 Gaussian-Mixture-Model (GMM) based Clustering

Code

from sklearn.mixture import GaussianMixture

bic = []
models = []
for k in range(1, 10):  # test up to 9 clusters
    model = GaussianMixture(n_components=k, covariance_type='full', random_state=2025)
    model.fit(X)
    bic.append(model.bic(X))
    models.append(model)

GaussianMixture(n_components=9, random_state=2025)

In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.

Code

# Choose model with lowest BIC
best_model = models[np.argmin(bic)]
best_model

GaussianMixture(n_components=3, random_state=2025)

Code

labels = best_model.predict(X)
labels

array([0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
       0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
       0, 0, 0, 0, 0, 0, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
       2, 2, 2, 2, 1, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
       2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
       1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
       1, 2, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1])

Code

plt.figure(figsize=(8, 6))
plt.scatter(X[:, 0], X[:, 1], c=labels)
plt.tight_layout()